Huvudinnehåll
Utforska ett ämne i kunskapsbanken
Meteorologi
Faktapaket: Meteorologiska modeller
Ensembleprognoser
På grund av osäkerheten i indata och att atmosfären är icke-linjär går det inte att göra exakta förutsägelser av vädret. Detta leder till att se väderprognoser som ett sannolikhetsproblem.
Meteorologiska prognoser är inte, och kommer aldrig att kunna bli, exakta förutsägelser av det framtida vädret. Den grundläggande orsaken till detta är att atmosfären är ett kaotiskt system.
Detta innebär att felet i väderprognoser baserade på numeriska väderprognosmodeller ökar med ökad prognoslängd för att efter någon vecka eller så sakna någon likhet med det verkliga vädret. För att exemplifiera hur denna feltillväxt i väderprognosmodellerna uppkommer kan man betrakta följande enkla modell baserad på den icke-linjära ekvationen:
Y(n+1) = a·Y(n) - Y(n)²
Ekvationen bestämmer hur variabeln Y (t ex temperaturen i en viss punkt) vid en framtida tidpunkt n+1 beror av värdet på Y vid tidpunkten n och på en parameter a. Denna ekvation är som synes väldigt enkel och naturligtvis inte en modell av den verkliga atmosfären.
Trots det liknar den ändå de ekvationer som bestämmer det verkliga vädrets utveckling i den meningen att den är icke-linjär och att den stegar sig fram i tiden med diskreta steg. Man kan visa att om parametern a ligger i intervallet 0 ≤ a ≤ 4 och om startvärdet för variabeln (Y(0)) ligger i intervallet 0 ≤ Y(0) ≤ a så kommer Y för all framtid, dvs för alla n, att ligga i intervallet 0 ≤ Y(n) ≤ a.
Detta innebär att variabeln Y har den realistiska egenskapen att den aldrig kan bli väldigt stor, utan håller sig, som lufttemperaturen, inom ett visst intervall. Om parametern a har värdet 3.75 och startvärdet för Y har värdet 1.5 får man en tidsutveckling av Y som kan ses i den vänstra kolumnen i tabellen nedan.
Tidsutvecklingen av Y synes vara slumpmässig från ett tidssteg till ett annat trots att den bestäms av en deterministisk ekvation och inga tecken på periodicitet kan urskiljas. I denna beräkning har alla värden rundats av till fyra gällande decimaler. Betrakta nu denna sekvens som den ”sanna” utvecklingen.
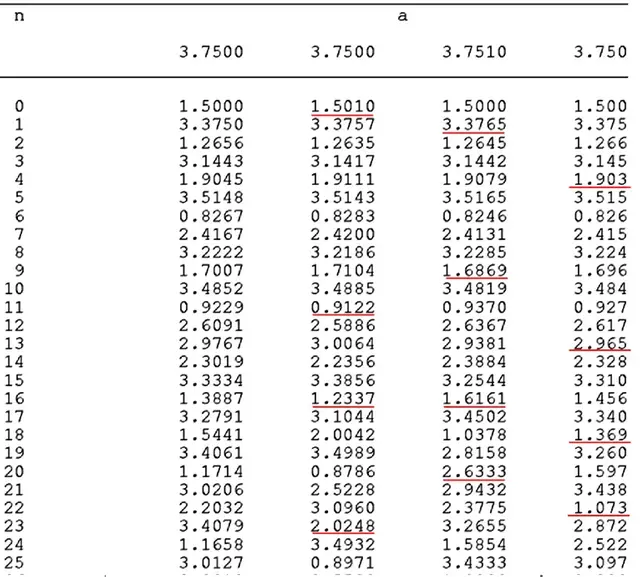 Förstora bilden
Förstora bildenNumeriska lösningar Y(n) till den icke-linjära ekvationen Y(n+1) = a·Y(n) - Y(n)² för olika värden på parametern a och initialvärdet Y(0). Det antal signifikanta siffror som använts i beräkningarna är desamma som anges
Vi kommer aldrig att exakt kunna bestämma atmosfärens tillstånd vid en viss tidpunkt. Dels för att varje är mätning behäftad med ett visst fel och dels för att det är omöjligt att mäta vid ett oändligt antal punkter i tid och rum. Vår ofullständiga kunskap om atmosfärens initiala tillstånd ger därför upphov till ett fel i starttillståndet, som när man stegar sig fram i tiden i de operationella väderprognosmodellerna amplifieras och ger upphov till en feltillväx.
Vi kan i modellen (1) efterlikna denna process genom att i stället för det korrekta värdet 1.5 för startvärdet sätta det till 1.501. Man får då den tidsutveckling som ges i den andra kolumnen i tabellen. Skillnaden mellan den första och andra kolumnen, dvs felet, ökar stadigt och den första gången som felet överstiger 0.001, 0.01, 0.1 och 1.0 är understrukna. Feltillväxten är något oregelbunden, men i medeltal tar det 7 till 8 tidssteg innan felet har ökat med en faktor 10, dvs feltillväxten är ungefärligen exponentiell.
Väderprognosmodeller kommer alltid att vara approximativa modeller av den verkliga atmosfären. Ett av många skäl till detta är att modeller alltid kommer att ha en finit upplösning i tid och rum, vilket innebär att det alltid kommer att finnas småskaliga (i tid och rum) fenomen som inte är explicit upplösta i modellen. Detta leder ofrånkomligen till att fel uppkommer.
För att efterlikna detta förhållande i den enkla modellen (1) ändras parametern a lite grann till 3.751 medan startvärdet sätts tillbaka till det korrekta värdet 1.5. Som framgår av nästa kolumn i tabellen så ökar felet även i detta fall oregelbundet och ungefär lika snabbt som i föregående fall.
Om felet är i initialtillståndet eller i modellen verkar alltså vara oväsentligt. Detta är konsistent med det faktum att ett modellfel oundvikligen kommer att introducera ett fel, och när detta fel väl uppkommer kommer det att växa till på likartat sätt som om det hade funnits där redan från början.
Den sista kolumnen i tabellen illustrerar vad som händer i det hypotetiska fallet att vi har både en perfekt modell och en exakt specificering av initialtillståndet, trots att detta som sagt är omöjligt. På grund av det oundvikliga faktum att en dator är begränsad att räkna med ett finit antal gällande decimaler kommer avrundningsfel alltid att uppkomma. Detta efterliknas i modell (1) genom att alla värden avrundats till tre i stället för fyra gällande decimaler. Som synes får man även i detta fall en feltillväxt som är jämförbar med de övriga fallen.
Ensembleprognossystem
Drömmen om att en dag kunna göra perfekta prognoser måste alltså överges – det är omöjligt. Hur bra modellen än är och hur bra initialtillståndet än kan specificeras så kommer prognoserna obönhörligen att avlägsna sig från den verkliga väderutvecklingen.
Två lika rimliga uppskattningar om hur initialtillståndet ser ut, och/eller två lika rimliga modell-designer, kommer att ge upphov till två olika prognoser som efter hand kommer att avlägsna sig från varandra. Denna insikt leder till att det bästa man kan göra är att framställa ett helt kluster av prognoser – baserade på olika, men lika rimliga uppskattningar om hur initialtillståndet ser ut och/eller lika rimliga modell-designer.
Ju fler medlemmar som ett sådant kluster består av, ju bättre de olika modell-designerna liknar den verkliga atmosfären och ju bättre de olika initialtillstånden reflekterar det sanna initiala atmosfärstillståndet, desto större är sannolikheten att den verkliga väderutvecklingen finns någonstans ibland detta kluster av prognoser.
För att i verkliga väderprognosmodeller uppskatta hur det potentiella utfallet av olika väderutvecklingar skulle kunna gestalta sig har man därför utvecklat så kallade Ensemble Prognos System (EPS) enligt ovanstående idéer. Sådana system lämpar sig också till att kvantifiera hur felen utvecklar sig i tiden för en godtycklig medlem i klustret (eller en prognos framräknad som en funktion av klustermedlemmarna).
System av lika sannolika prognoser
I ett idealt EPS är de olika ensemblemedlemmarna beräknade från modeller och initialtillstånd som är lika sannolika approximationer av verkligheten. Varje prognos är därmed lika sannolik att vara den som bäst överensstämmer med den verkliga atmosfärens utveckling.
Vid en viss given prognoslängd kan man evaluera utfallet av prognoserna från de olika klustermedlemmarna genom att beräkna den relativa frekvensfördelningen. Denna används för att uppskatta det som primärt är EPS-systemets prognosinnehåll, nämligen sannolikhetsfördelningen (på engelska Probability Density Function = PDF).
En prognos i form av en sannolikhetsfördelning utgör den bästa uppskattning man kan göra om den verkliga utvecklingen. En sådan prognos är probabilistisk. Detta är en viktig kvalitativ skillnad gentemot en deterministisk prognos, vilket erhålles då man endast gör en prognos baserad på en modell och ett initialtillstånd.
Deterministisk prognos från sannolikhetsfördelningen
Trots att prognosen logiskt sett bör presenteras som en sannolikhetsfördelning är det ändå ofta önskvärt att ur PDFen extrahera en specifik, deterministisk, prognos. Den oftast förekommande deterministiska prognosen framställd på detta sätt är baserad på väntevärdet, eller medelvärdet, av PDFen. En annan möjlighet är att välja den medlem som ligger närmast det största värdet på den uppskattade PDFen (det s k typvärdet), då denna utgör den bästa uppskattningen på den enskilt mest sannolika prognosen.
Hur meningsfulla prognoser av denna typ är beror dock på den specifika form som den aktuella PDFen har. För korta prognoser då prognoskvaliteten normalt sett är hög är sannolikhetsfördelningen väl samlad och hoptryckt kring medelvärdet och liknar oftast en normalfördelning.
Det hela är då ganska oproblematiskt, t ex har en normalfördelning samma vänte- och typvärde. För längre prognoslängder kan dock PDFen få ett mer komplicerat utseende vilket försvårar specifikationen av en meningsfull deterministisk prognos. Ett exempel är en bimodal PDF med två distinkta maxima av samma storlek separerade av ett djupt minimum.
I stället för en deterministisk prognos har man då två lika sannolika prognoser (typvärden). En prognos baserad på medelvärdet å andra sidan vore i detta fall helt missvisande då den är ytterst osannolik.
Svårt att utvärdera
En fundamental svårighet med sannolikhetsprognoser är att en sådan prognos för ett enskilt, specifikt tillfälle inte kan verifieras. Den verkliga atmosfären utvecklar sig ju endast på ett sätt (en realisation) medan prognosen utgörs av en PDF baserad på många realisationer.
Vad som skulle erfordras är en uppsättning parallella jordar med atmosfärer som vid initialtillfället till synes är identiska, men på grund av små slumpmässiga orsaker utvecklar sig lite annorlunda från varandra (många realisationer). I avsaknad av denna ideala situation står man inför dilemmat att det är omöjligt att verifiera en PDF (från modell) med en enstaka realisation (från den verkliga atmosfären).
Sannolikhetsprognoser kan därför bara evalueras från ett statistiskt perspektiv, genom att jämföra sannolikhetsprognosernas statistiska egenskaper över en viss tidsperiod med motsvarande egenskaper hos den verkliga atmosfären.
Kontrollanalys
I verkligheten har det visat sig vara svårt att framställa en uppsättning lika sannolika initialtillstånd som var och en har samma kvalitet som det initialtillstånd som är resultatet av dagens bästa analystekniker. Det förfarande som för närvarande vanligtvis används är att man utgår från det initialtillstånd som resulterar från användandet av dagens bästa analystekniker. Detta initialtillstånd kallas kontrollanalysen. Till kontrollanalysen adderar man små störningar för att på så vis erhålla störda, eller perturberade, analyser. Var och en av dessa perturberade analyser är dock sinsemellan à priori lika goda och sannolika uppskattningar av atmosfärens verkliga tillstånd.
Var och en av dessa är dock, definitionsmässigt, en sämre uppskattning än kontrollanalysen av hur den verkliga atmosfären ser ut. Vi vet alltså à priori att den prognos som utgår från kontrollanalysen är en bättre prognos än de som utgår från de perturberade analyserna (i alla fall i början av prognosen).
Ett alternativ till att utnyttja vänte- eller typvärdet av PDFen för att erhålla en deterministisk prognos är att helt enkelt utnyttja prognosen som utgår från kontrollanalysen. Osäkerheten i denna deterministiska prognos kan då uppskattas från spridningen inom klustret av prognoser startande från de perturberade initialtillstånden. Hur stor spridningen blir, och därmed osäkerheten i prognosen, är en direkt följd av hur snabbt två närliggande lösningar till modellen divergerar. Denna divergens beror i hög grad på varje initialtillstånds speciella karakteristik, men också på realismen på den modell av atmosfären som används.
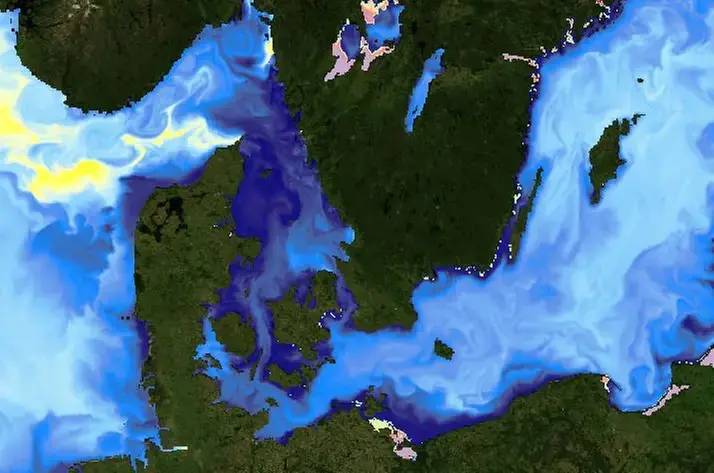
Ett exempel på hur en prognos baserad på denna metodik kan se ut visas i figuren nedan. Förutom själva prognosen, i detta fallet strömningen i mellersta troposfären, ges också uppskattningar på hur stor osäkerheten är, här markerat med skuggning i olika färger.
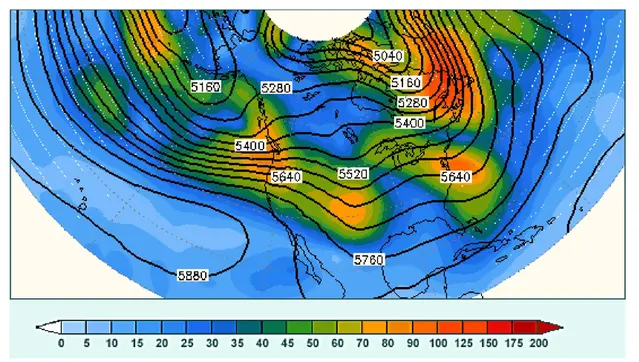 Förstora bilden
Förstora bildenEn 84-timmars prognos av höjden till tryckytan 500 hPa giltig för tidpunkten 22 november 2001 kl. 1200 UTC utgående från analyser vid tidpunkten 19 november 2001 kl. 0000 UTC. Förutom själva prognosen, markerade med svarta isolinjer, ges också uppskattningar på hur stor osäkerheten är, här markerat med skuggning i olika färger.
Det finns många viktiga och intressanta frågeställningar som måste beaktas vid utformandet av ett EPS. Historiskt sett har specifikationen av de olika initialtillstånden för ett EPS tilldragit sig mycket uppmärksamhet.
Det ska här poängteras att antalet variabler som måste specificeras i initialtillståndet till en modern väderprognosmodell är av storleksordningen 108 eller större, dvs avsevärt större än det enda värdet i ekvation (1) ovan.
En till synes rimlig metod för att skapa olika initialtillstånd är att addera små slumpmässiga störningar till samtliga 108 variabler i den operationella analysen som modellen i vanliga fall använder som initialtillstånd. Med ”små” menas att de skall vara av samma storleksordning som typiska analysfel.
Det visar sig dock att denna s k ”Monte Carlo” metod inte är särskilt lyckad ur praktisk synvinkel. Anledningen är att divergenshastigheten mellan de olika prognoserna blir för liten, vilket medför att det dröjer väldigt länge innan de olika prognoserna skiljer sig åt markant - så länge att prognoskvaliteten då är så dålig att prognosen är oanvändbar och därmed ointressant.
Det är alltså nödvändigt att störningarna har en viss struktur för att de olika prognoserna ska divergera på ett realistiskt sätt. För att klargöra vad som menas med detta kan man återknyta till experimenten med modellen (1) såsom redovisade i tabellen ovan.
Divergenshastigheten mellan var och en av de ”störda” experimenten och den ”sanna” utvecklingen var ungefärligen exponentiell, där felet ökade med en storleksordning vart 7:e till 8:e tidssteg. Samma divergenshastighet ska nu finnas sinsemellan var och en av de störda experimenten. Flera olika tekniker för att ta fram störningar med dessa egenskaper har utvecklats och använts i operationella EPS-system.
De mest namnkunniga är breeding-tekniken som utvecklats vid den amerikanska vädertjänsten (NCEP) och singular vector-tekniken, utvecklad vid ECMWF. Även om dessa tekniker båda klarar av att producera ensemblemedlemmar som divergerar från varandra med realistisk hastighet är de långt ifrån idealiska.
Det kanske allvarligaste problemet är att de saknar en direkt koppling till osäkerheten i analysen, vilket ju är den grundläggande felkällan. Arbete med metodiker som explicit tar hänsyn till osäkerheterna i specifikationen av initialtillståndet pågår för närvarande för fullt,
Mer i detta faktapaket
- Meteorologi
Meteorologiska modeller
Prognosmodeller och kraftfulla datorer är grunden för dagens prognoser. Det finns många olika modeller som används för olika typer av prognoser.
- Meteorologiska modeller
Dataassimilering
Med hjälp av dataassimilering skapas startvärden (väderläget) för en numerisk prognosmodell. Det är en av de viktigaste komponenterna i ett prognos...
- Meteorologiska modeller
De första stegen mot numeriska prognoser
År 1956 gjordes de första datorbaserade prognoserna vid SMHI, men vägen dit var lång.
- Meteorologiska modeller
Hur är en numerisk väderprognosmodell uppbyggd?
Väderprognosproblemet är ett fysikaliskt problem, som kan formuleras matematiskt, som ett system av differentialekvationer. Här diskuteras själva p...
- Meteorologiska modeller
Kalmanfiltrering av numeriska prognoser
Kalmanfiltrering är en matematisk metod att optimalt bestämma statistiska parametrar ur ett begränsat antal observationer. Adaptiva filter är kraft...
- Meteorologiska modeller
Kaos - centralt för väderprognoser
En numerisk väderprognosmodell uppför sig kaotiskt eftersom den innehåller icke-linjära termer. Det innebär att en mycket liten ändring av exempelv...
- Meteorologiska modeller
Korta nederbördsprognoser - KNEP
SMHI har utvecklat en metod för att göra korta nederbördsprognoser med hjälp av senaste radarinformationen.
- Meteorologiska modeller
Markens roll i en numerisk prognosmodell
Inte bara atmosfären utan även markytan och haven måste modelleras i en väderprognosmodell.
Faktapaket meteorologi
Alla faktapaket inom meteorologi
Vi har satt ihop artiklar utifrån kategorier. Allt för att du ska få ett samlat innehåll.