Huvudinnehåll
Utforska ett ämne i kunskapsbanken
Meteorologi
Faktapaket: Meteorologiska modeller
Hur är en numerisk väderprognosmodell uppbyggd?
Väderprognosproblemet är ett fysikaliskt problem, som kan formuleras matematiskt, som ett system av differentialekvationer. Här diskuteras själva prognosmodellen, men en lika central del av ett numeriskt prognossystem är hur startvärden skapas, genom en process som heter dataassimilering.
Matematisk formulering av väderprognosproblemet
Jordens atmosfär utgörs av en gasblandning av torr luft, som huvudsakligen består av kväve och syre, samt vattenånga. Dessutom finns det koldioxid, som är av fundamental betydelse för vårt klimat.
Atmosfären innehåller också hydrometeorer, såsom molndroppar och iskristaller, vilket kan omvandlas till nederbörd. Även aerosoler och luftföroreningar har en påverkan på vädret. Vi tillämpar Newtons andra lag (F=a·m), på en enhetsmassa luft (1 kg), och utrycker accelerationen som summan av alla krafter som verkar på luftpaketet:
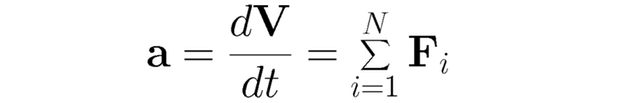 Förstora bilden
Förstora bildenNewtons andra lag (F=a*m) tillämpas, på en enhetsmassa luft (1kg), och utrycker accelerationen som summan av alla krafter som verkar på luftpaketet. Numerisk väderprognosmodell
vilket ger
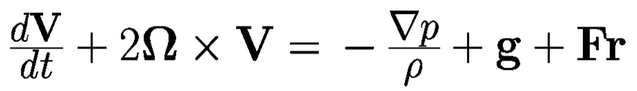 Förstora bilden
Förstora bildenTillämpning av Newtons andra lag (F=a*m) tillämpas, på en enhetsmassa luft (1kg), och utrycker accelerationen som summan av alla krafter som verkar på luftpaketet. Numerisk väderprognosmodell
Här är den andra termen Corioliskraften, som avlänkar rörelsen till höger på norra halvklotet, till vänster på södra och saknas vid ekvatorn. Den är proportionell mot vindhastigheten och beror på jordens rotation.
Till höger om likhetstecknet finns tryckgradientkraften som accelererar luften mot lägre tryck, samt gravitationen g. Fr står för andra processer som till exempel friktion (turbulens), som är stor nära marken samt i övre delen av troposfären (ca 8-10 km), där det förekommer stora vertikala variationer av vindhastigheten. I vertikal led antas oftast hydrostatisk balans:
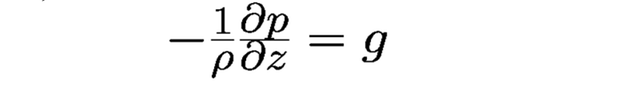 Förstora bilden
Förstora bildenHydrostatisk balans antas oftast i matematiska formuleringar av väder.
Denna approximation innebär att trycket i en nivå endast är beroende av massan av luften som finns ovanför. Det betyder bland annat att ljudvågor inte kan beskrivas, eftersom trycket där innehåller lokala kompressioner.
Hydrostatisk balans gäller om den horisontella skalan >> vertikala skalan. Det betyder att vi inte kan anta detta för processer som har liten horisontell utsträckning, exempelvis konvektion (cumulusmoln, regnskurar). I mesoskaliga (högupplösta) modeller görs inte antagandet om hydrostatisk balans.
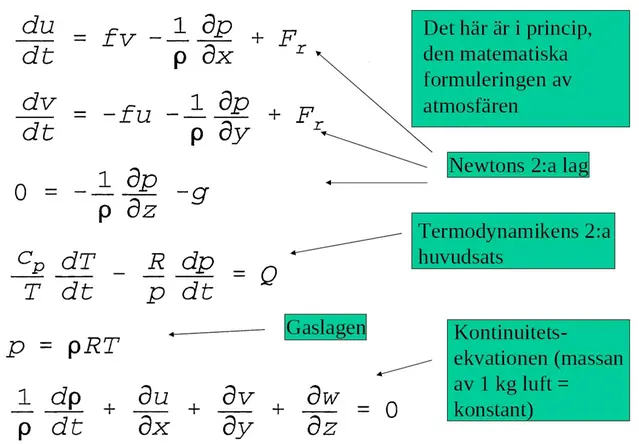
Andra ekvationer som används är termodynamikens andra huvudsats, gaslagen och kontinuitetsekvationen. Om vi delar upp vindhastigheten i tre komponenter, u,v och w, kan hela atmosfären beskrivas av följande system:
 Förstora bilden
Förstora bildenMatematisk beskrivning av atmosfären bestående av Newtons andra lag, termodynimikens andra huvudsats och kontinuitetsekvationen.
Variablerna i systemet ovan är:
- u = vindkomponent i ost-västlig riktning (x-led) >0 för riktning mot öster
- v = vindkomponent i nord-sydlig riktning (y-led) >0 för riktning mot norr
- w = vertikalvind >0 för uppåt (z-led)
- T = luftens temperatur
- f = 2Ω sin φ, Coriolisparametern, där Ω är jordens rotationshastighet och φ är latituden
- ρ = luftens densitet
- p = luftens tryck
- Cp = luftens specifika värme
- R = gaskonstanten för luft
Termerna Fr har redan nämnts, och Q är värmekällor för luften exempelvis kondensationsvärme och absorption av strålning. I ekvationssystemet saknas fuktigheten och diverse hydrometeorer, som molnvatten och molnis, samt turbulent kinetisk energi.
Problemet inom fluidmekaniken är icke-linjäriteten
Icke-linjära processer gör att energi kan överföras till andra skalor, beskrivet i följande poem: "Big whirls have little whirls who feed upon their velocity, and little whirls have lesser whirls, and so on to viscocity." Detta beskriver den så kallade kaskadprocessen hur energin transformeras från större skalor till allt mindre.
Icke-linjära processer är kaotiska, och detta sätter gränser för hur långa prognoser som kan göras. Det ovan beskrivna ekvationssystemet är icke-linjärt. Låt oss se närmare på en icke-linjär term. Om man låter temperaturen T vara en funktion av en rumsdimension och tiden, dvs. T=T(x,t) kan vi skriva:
 Förstora bilden
Förstora bildenExempel på icke-linjär term
Fysikaliskt tolkas detta uttryck som att temperaturförändringen i en punkt (x=konstant) beror på två termer. Den sista termen säger att om temperaturen är högre längre bort (större x) och det blåser mot punkten ifråga (u<0) kommer temperaturen i punkten att öka. Samtidigt säger den första termen att temperaturen kommer ändras i punkten om luftpaketet uppvärms eller kyls på vägen.
Icke-linjäriteten ligger i att den sista termen är en produkt av två beroende variabler i systemet. Man kan alltså sätta in ovanstående uttryck i termodynamikens andra huvudsats, (och detsamma med andra termer) och får då en så kallad Eulersk formulering av ekvationssystemet, uttryckt i partiella derivator. Detta icke-linjära system måste lösas med hjälp av numeriska metoder. Här beskrivs en Eulersk formulering, men även andra formuleringar kan användas.
Numerisk formulering på ett rutnät
Man delar in ett prognosområde i ett rutnät som kallas gridnät, både horisontellt och vertikalt, där alla variabler initialt tilldelats ett medelvärde över gridrutan (dataassimilering). Man får då ett så kallat diskret system, med en mängd olika variabler vars utveckling ges i differensform. Man beräknar förändringen under ett tidssteg (några minuter), och erhåller då väderläget efter detta tidssteg. Detta upprepas till prognoslängdens slut.
De termer som står till höger om likhetstecknet i systemet ovan, är olika fysikaliska processer som beräknas i särskilda program, varje tidssteg, så kallade parametrisering. Numeriska prognosmodeller är följaktligen mycket datorkrävande. Det finns, som nämnts ovan, andra numeriska lösningsmetoder, till exempel kan diskretiseringen göras genom spektrala metoder (exempelvis genom Fourieranalys).
Globala och regionala prognosmodeller
Då vädret är globalt, är det naturligt att definiera hela jorden som ett prognosområde. Detta görs också på många ställen, exempelvis på det Europeiska vädercentret, ECMWF. Det är mycket datorkrävande, inte minst för att dataassimilationen utnyttjar observationer över hela globen.
Om man gör kortare prognoser kan man välja att göra en regional modell, vars storlek beror på prognoslängden, där värden på ränderna kommer från en global modell, exempelvis AROME
Prognoser över ett begränsat område
Fördelar
- Litet område att analysera
- Litet område att prognosera (råd med hög upplösning)
- Täta analysintervall
Nackdelar
- Både initialvärdesproblem och randvärdesproblem = matematiskt illa ställt problem, löses ofta pragmatiskt genom en relaxationszon nära randen.
- Starkt beroende av rändernas kvalitet
- Begränsad prognostid
Utvecklingen går mot allt högre upplösning i modellerna, och detta kräver att de fysikaliska och numeriska metoderna utvecklas allt mer, men fortfarande finns det stora osäkerheter då det gäller detaljer i moln och nederbördsprocesser.
Mer i detta faktapaket
- Meteorologi
Meteorologiska modeller
Prognosmodeller och kraftfulla datorer är grunden för dagens prognoser. Det finns många olika modeller som används för olika typer av prognoser.
- Meteorologiska modeller
Dataassimilering
Med hjälp av dataassimilering skapas startvärden (väderläget) för en numerisk prognosmodell. Det är en av de viktigaste komponenterna i ett prognos...
- Meteorologiska modeller
De första stegen mot numeriska prognoser
År 1956 gjordes de första datorbaserade prognoserna vid SMHI, men vägen dit var lång.
- Meteorologiska modeller
Ensembleprognoser
På grund av osäkerheten i indata och att atmosfären är icke-linjär går det inte att göra exakta förutsägelser av vädret. Detta leder till att se vä...
- Meteorologiska modeller
Kalmanfiltrering av numeriska prognoser
Kalmanfiltrering är en matematisk metod att optimalt bestämma statistiska parametrar ur ett begränsat antal observationer. Adaptiva filter är kraft...
- Meteorologiska modeller
Kaos - centralt för väderprognoser
En numerisk väderprognosmodell uppför sig kaotiskt eftersom den innehåller icke-linjära termer. Det innebär att en mycket liten ändring av exempelv...
- Meteorologiska modeller
Korta nederbördsprognoser - KNEP
SMHI har utvecklat en metod för att göra korta nederbördsprognoser med hjälp av senaste radarinformationen.
- Meteorologiska modeller
Markens roll i en numerisk prognosmodell
Inte bara atmosfären utan även markytan och haven måste modelleras i en väderprognosmodell.
Faktapaket meteorologi
Alla faktapaket inom meteorologi
Vi har satt ihop artiklar utifrån kategorier. Allt för att du ska få ett samlat innehåll.