Parametrisering

Förutom de dynamiska ekvationerna, som styr vädrets utveckling i stort, påverkas vädret även av andra mer eller mindre viktiga faktorer, på mindre skalor.

I atmosfären sker det en lång rad olika processer med olika skalor i både tid och rum, alltifrån de tusentals kilometer långa vågor som styr vädrets växlingar från dag till dag och ner till små virvlar av t.ex. vissna löv. Ja ännu längre, de vattendroppar som bildar moln, regn och snö är bara någon tusendels millimeter stora – och ljusets våglängd är ju ännu kortare.

I princip kan alla dessa processer beskrivas matematiskt och därigenom beräknas ("prognoseras") med hjälp av datorprogram. Men i praktiken är det naturligtvis omöjligt att hålla reda på varenda molndroppe, och man är inte heller särskilt intresserad av att känna till och beräkna varenda liten luftvirvel från t.ex. en nysning.

Vi har redan sett hur de datorprogrammerade vädermodellerna delar in atmosfären i små rutor som kan vara hundratals kvadratkilometer stora och i tio- eller hundratals meter tjocka vertikala skikt. En sådan volym kan vi kalla en 'gridvolym'.

I vädermodellen beskrivs förhållandena ("vädret") i varje gridvolym av ett litet antal modellparametrar såsom vind, temperatur, fuktighet, moln, ozon, och kanske mängden av några luftföroreningar. Men inne i varje volym sker alltså en hel rad processer som inte kan beskrivas i detalj. I stället försöker man uttrycka hur de beror på modellparametrarna, man säger att man "parametriserar" dem.

Tre viktiga processer

Små luftvirvlar, turbulens, är en av de viktigaste processerna. Även om man alltså inte kan beräkna varenda virvel, är det nödvändigt att ta hänsyn till deras nettoeffekt eftersom det är turbulensen som ombesörjer en stor del av värmeutbytet mellan luften och den underliggande terrängen.

När solen skiner värms marken upp och det bildas små blåsor av varmluft som stiger uppåt och blandas in och värmer atmosfären. För att parametrisera turbulensen gör man oftast en statistisk modellering av avvikelserna från modellparametrarna; om t.ex. Tm är medeltemperaturen i gridvolymen och T´ är avvikelserna från Tm inne i volymen beskriver man den 'verkliga' temperaturen som T= Tm+ T´ Avvikelserna T´ uttrycker man, på mer eller mindre sofistikerade sätt, som enbart beroende på Tm och de andra modellparametrarna ('medelvärdena') i gridvolymen.

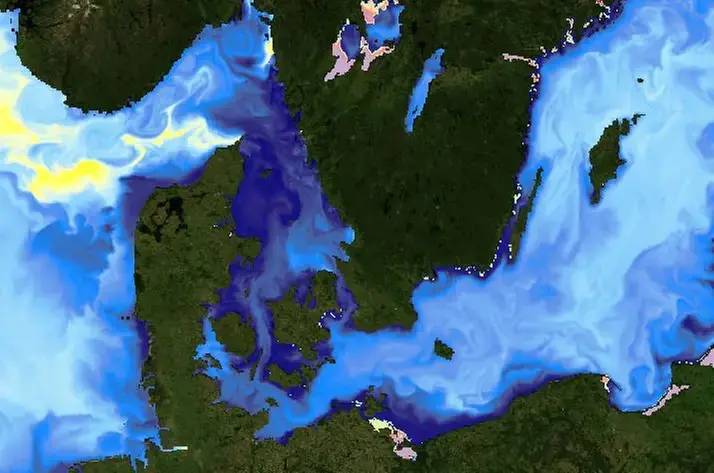
Moln och nederbörd beskriver man också med hjälp av några få modellparametrar till exempel mängden molnvatten i kilogram per kilogram luft. Molnvattenmängden parametriseras som beroende på gridvolymens temperatur, fuktighet (vattenånghalten) och så vidare.

Den tredje nödvändiga parametriseringen är behandlingen av strålningen, både den kortvågiga från solen och den långvågiga värmestrålningen från marken och luften. Beroende på våglängden absorberas och emitteras strålning mer eller mindre av luftens molekyler.

Några välkända fysikaliska lagar beskriver hur absorbtionen och emissionen beror på luftens (medel)temperatur och halterna av vattenånga, koldioxid och ozon, och modellen beräknar ("parametriserar") effekterna av strålningen på medelvärdena i gridvolymerna.

I de klimatscenarier som publiceras av IPCC har man gjort precis likadana strålningsparametriseringar där man ändrar modellatmosfärernas halter av koldioxid. Här arbetar vi inom främst två områden, molnens och markens fysik.