Huvudinnehåll
Utforska ett ämne i kunskapsbanken
Klimat
Faktapaket: Historiskt klimat
Hur beräknas utjämnade långtidsmedelvärden?
I diagram som illustrerar utvecklingen av exempelvis temperaturen eller nederbörden är det vanligt att även presentera en kurva som visar ett långtidsmedelvärde som ger en utjämnad bild av förloppet. Här beskrivs två olika varianter av beräkningar av långtidsmedelvärden samt deras för- och nackdelar.
Långtidsmedelvärden används för att enklare kunna se om det förekommer någon förändring eller trend i de data som presenteras. Innehåller datamaterialet stora variationer kan det vara svårt att med blotta ögat se om det finns någon avtagande/stigande trend under exempelvis det senaste årtiondet. Det huvudsakliga syftet med kurvan är därför att grafiskt illustrera förloppet på ett utjämnat sätt. Observera att man utifrån långtidsmedelvärden inte kan veta om någon trend är statistiskt signifikant eller ej, då krävs djupare analyser.
Löpande medelvärden
Det enklaste sättet att beräkna långtidsmedelvärden är att beräkna löpande medelvärden där alla år inom perioden får lika stor vikt. De kan ha olika tidslängd men 10-års perioder är vanligt förekommande.
 Förstora bilden
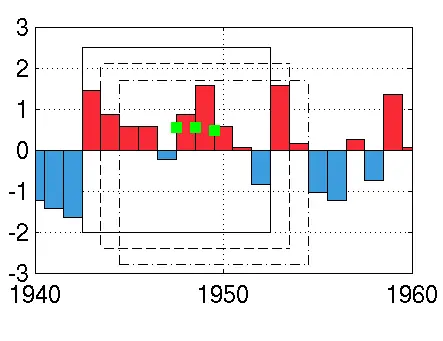
Förstora bildenRespektive rektangel visar vilka data som används i ett 10-års löpande medelvärde. Motsvarande medelvärde som är markerade med gröna fyrkanter har placerats i mitten av tioårsperioden. Rektangeln löper sedan genom hela dataserien.
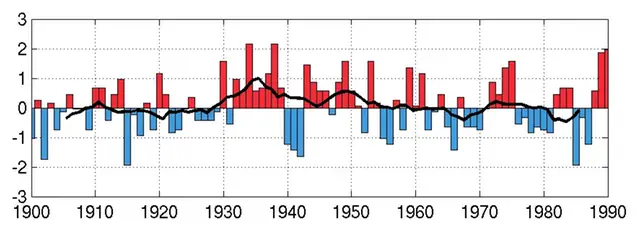
I exemplet nedan har ett löpande medelvärde beräknats på detta sätt. Det första värdet i den svarta linjen är alltså medelvärdet för 1901-1910 och det sista för 1981-1990.
 Förstora bilden
Förstora bildenDen svarta heldragna linjen motsvarar ett löpande 10-års medelvärde.
10-åriga löpande medelvärden presenteras ibland (tex i Excel) så att medelvärdena anges för det sista året i 10-årsserien. Grafiskt betyder det att kurvan förskjuts framåt med 5 år.
Långtidsmedelvärde beräknat med Gaussfilter
Ett annat sätt att beräkna långtidsmedelvärden är att Gaussfiltrera data. Skillnaden i jämförelse med det löpande medelvärdet är att alla år i det här fallet inte får samma vikt. Vikterna för respektive år tas istället fram med hjälp av en normerad Gaussfunktion.
Funktionen (vikterna) får olika utseenden (värden) beroende på vilken standardavvikelse som används som ingångsvärde till Gaussfunktionen. Oberoende av vilken standardavvikelse som används är alltid summan av alla vikter lika med 1.
 Förstora bilden
Förstora bildenDen svarta och gråa heldragna linjen anger vikten för respektive år framtaget med Gaussfunktionen för standardavvikelsen 3 respektive 9. Summan av samtliga vikter är lika med 1. De svartmarkerade fält motsvarar åren utanför 10-års perioden och de gråmarkerade fält åren utanför 30-års perioden. Gaussfunktionen löper egentligen genom hela dataserien.
I exemplet i figuren ovan används standardavvikelsen 3 i den toppiga Gaussfunktionen. Då varierar vikterna från 0 till maximum 0.133. I långtidsmedelvärdet för år 1950 får år 1950 den maximala vikten, 0.133, åren 1949 och 1951 den näst högsta vikten, 1948 och 1952 den näst näst högsta vikten osv.
Perioderna i de svartmarkerade fälten i figuren ovan, före år 1945 och efter 1955, får minimala vikter. Summan av vikterna före 1945 och efter 1955 utgör endast cirka 6 % av den totala vikten.
När standardavvikelsen 3 används för att bestämma vikterna i Gaussfunktionen kan man säga att långtidsmedelvärdet ungefär motsvarar ett utjämnat förlopp motsvarande 10-års medelvärden (viktat med ett rektangulärt filter).
Då standardavvikelsen 9 istället används så är det cirka 30 år, 15 år före och 15 år efter vars vikter blir av betydelse för medelvärdet. Det benämns då som ett utjämnat förlopp motsvarande ungefär 30-års medelvärden.
 Förstora bilden
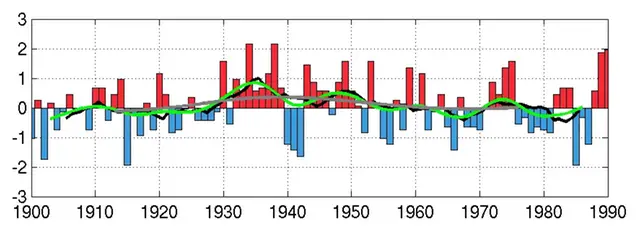
Förstora bildenDen gröna respektive gråa heldragna linjen visar medelvärdena då viktning gjorts med hjälp av Gaussfunktionen och standardavvikelsen 3 respektive 9. Den svarta heldragna linjen visar de beräknade löpande 10-års medelvärdena.
Skillnader
Som ses i figuren ovan så är skillnaden mellan löpande 10-års medelvärden (då medelvärdet presenteras i mitten av 10-års perioden) och medelvärden beräknade med Gaussfunktion motsvarande 10-års medelvärden inte så stor. De löpande 10-års medelvärdena är ”hackigare” medan medelvärdena beräknade med hjälp av Gaussfunktionen ger ett mer utjämnat förlopp.
Skillnaderna mellan de olika beräkningssätten är som störst då datamaterialet innehåller stora variationer från ett år till ett annat. I diagrammet ovan är det speciellt tydligt år 1940-1943 och 1982-1984. Här följer medelvärdet beräknat med Gaussfunktionen datamaterialet bättre. Fördelen med att använda medelvärden beräknade med Gaussfunktionen är att ett enstaka högt eller lågt värde inte får så stor genomslagskraft.
Start- och slutåren
Både när man använder 10-års löpande medelvärden och 10-års medelvärden beräknade med Gaussfunktionen blir det synbara problem med de första och sista 5 åren i en dataserie. För båda varianterna kommer medelvärdet för de första respektive sista 5 åren att bygga på färre antal år med hög vikt, därför kommer sannolikt medelvärdet för de 5 sista åren dessutom att förändras märkbart då en serie uppdateras med data för ytterligare år.
Hur man väljer att presentera start- och slutåren är en smaksak. Det enklaste är naturligtvis att inte alls presentera medelvärdet för de 5 första respektive sista åren. Dock är det oftast utvecklingen de sista åren som är mest intressant att följa. Därför presenteras ofta medelvärden för alla år. För att tydliggöra att medelvärdet då är osäkert för start- och slutåren kan man exempelvis markera det med prickad/streckad linje istället för heldragen, se figur nedan.
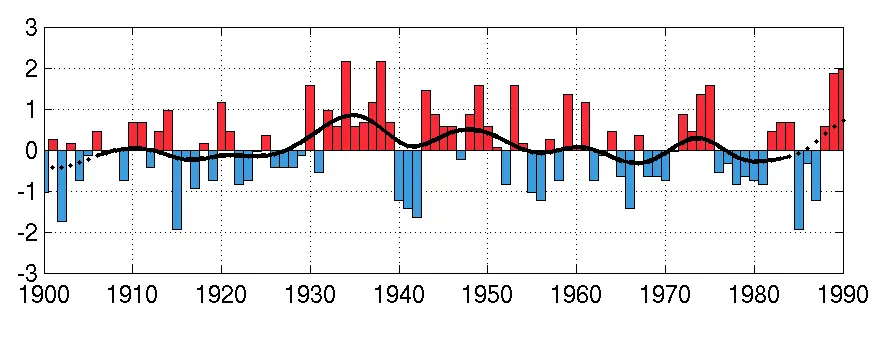
Exempel på långtidsmedelvärden, den svarta linjen, beräknade med hjälp av Gaussfunktionen som visar ett utjämnat förlopp motsvarande ungefär 10-års medelvärden. Start- och slutåren är markerade med prickad linje eftersom medelvärdena där bygger på färre antal år samt att de för slutåren kan komma att ändras när nya år tillkommer.
Mer i detta faktapaket
- Klimat
Historiskt klimat
Hur har temperatur och nederbörd i Sverige förändrats under lång tid? Kan man se någon förändring av salthalten i Östersjön? För att svara på de fr...
- Historiskt klimat
Beräkning av klimatindikatorn nederbörd
Beräkning av klimatindikatorn nederbörd Klimatindikatorn nederbörd beräknas med hjälp av över 1 200 tidsserier. Från dessa beräknas ett medelvärde...
- Historiskt klimat
Beräkning av klimatindikatorn temperatur
Beräkning av klimatindikatorn temperatur Klimatindikatorn temperatur baseras på över 450 tidsserier. Utifrån dessa beräknas medelvärden för år, må...
- Historiskt klimat
Återanalyser för atmosfären
Återanalyser för atmosfären Återanalyser produceras med hjälp av observationer och en väderprognosmodell och ger användaren information för platse...
- Historiskt klimat
Återanalyser för havet
Återanalyser för havet Återanalyser produceras med hjälp av observationer och en havsmodell och ger användaren information på platser och vid tidp...
Faktapaket klimat
Alla faktapaket inom klimat
Vi har satt ihop artiklar utifrån kategorier. Allt för att du ska få ett samlat innehåll.