Den förunderliga corioliseffekten

När temperaturskillnader jämnas ut genom att varm luft förs mot kallare nejder, och kall luft mot varmare, sker det inte utan motstånd. Jordrotationen vrider vinden rakt åt höger på norra halvklotet, åt vänster på södra. Denna så kallade corioliseffekt upptäcktes för mer än 150 år sedan, men omges fortfarande av ett mystiskt töcken.

Gaspard Gustave Coriolis (1792-1843) var inte intresserad av atmosfären eller ens vår snurrande jord, utan av maskiner med roterande delar. Dessa är utsatta för centrifugalkrafter som, om de är tillräckligt starka, kan slita sönder maskinen.

Coriolis var intresserad av att beräkna centrifugalkraften på ett föremål som, samtidigt som det deltar i rotationen, också rör sig relativt denna. Han fann att den vanliga centrifugalkraften måste kompletteras med en "tilläggskraft", vinkelrät mot rörelsen och proportionell mot hastigheten och rotationen. Den kom så småningom att bära hans namn.

Vi meteorologer är intresserade av Coriolis' "tilläggskraft" därför att vi lever på ett jättelikt snurrande klot, vilket påverkar luftens rörelser.

Jorden tillplattad vid polerna

En ort på Stockholms latitud rör sig med en hastighet av 220 m/s. Med ett avstånd till jordaxeln på 3100 km ger det en centrifugalacceleration som på en minut skulle förflytta ett löst föremål 20 meter i horisontell riktning, söderut (bort från jordaxeln). Men varför ser vi inga yttringar av detta?

Orsaken är att jordrotationen i tidernas begynnelse förändrade jordens form så att den blev "uppsvälld" där den roterar som fortast vid ekvatorn och tillplattad där den roterar långsammast vid polerna.

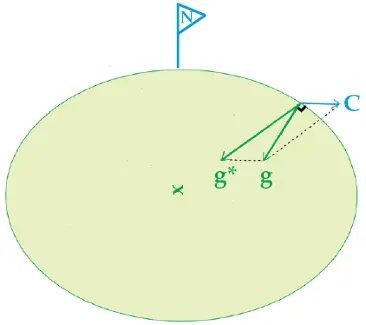
En följd av jordens tillplattning är att dragningskraften i allmänhet inte pekar rakt ner (vinkelrätt) mot jordytan utan en aning inåt, mot jordaxeln (se figur 1). På norra halvklotet innebär det en liten dragning mot norr.

Den tyngdkraft som vi upplever dagligen pekar däremot "rakt ner", ty den utgör summan av dragningskraften och den av rotationen skapade centrifugalkraften.

Men tyngdkraften pekar "rakt ner" bara om vi står stilla. Rör vi oss får en av de två krafterna, dragningskraften eller centrifugalkraften, överhanden och drar oss mot, respektive bort från jordaxeln. Denna sidoacceleration, förorsakad av jordrotationen och ökande med latituden, är just "corioliseffekten".

Med eller mot jordens rotation

Om vi springer österut, det vill säga i samma riktning som jorden snurrar, med en hastighet av 10 m/s, får vi en aning högre total hastighet än jorden (220+10=230 m/s). Vi påverkas därmed av en något förstärkt centrifugalkraft, som på en minut skulle förflytta oss 2 meter mot ekvatorn, alltså söderut.

Den förstärkta centrifugalkraften driver oss ännu starkare söderut, alltså till höger, vinkelrätt mot vår rörelse. Springer vi västerut, mot jordens rotation, blir vår hastighet lägre (220-10=210 m/s) och vi påverkas av en något försvagad centrifugalkraft, som dock fortfarande är riktad söderut.

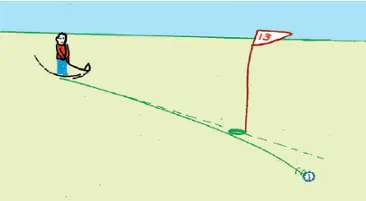
Försvagningen gör dock att balansen rubbas. Den norrut riktade dragningskraften får nu överhanden och driver oss på en minut 2 meter mot norr, sidledes och till höger, vinkelrätt mot vår rörelse. Man kan visa att vi får en sådan avlänkning till höger i förhållande till rörelseriktningen även när vi rör oss i såväl nord-sydliga som övriga riktningar ( figur 2).

Endast inom roterande system

Sammanfattningsvis gäller att corioliskraften på en kropp i rörelse är proportionell mot dess hastighet och alltid vinkelrät mot rörelseriktningen. Den kan därför bara ändra rörelseriktningen hos en kropp, inte dess hastighet. Den är noll vid ekvatorn och ökar ju närmare polerna vi kommer.

Liksom centrifugalkraften är corioliskraften ingen "vanlig kraft" som tyngdkraften eller de magnetiska och elektriska krafterna. Dessa finns så att säga alltid, medan centrifugalkraften och corioliskraften bara uppträder inom system som roterar, corioliskraften dessutom bara om ett föremål rör sig inom systemet.

Cirklar till slut

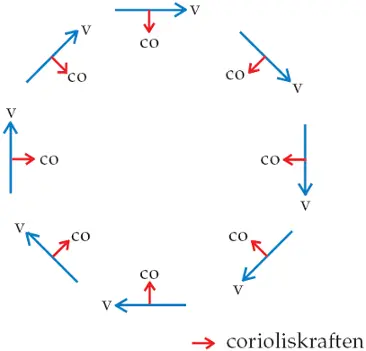
Ofta läser man att corioliskraften "avlänkar" ett föremåls rörelse, men det är inte hela sanningen. Rörelsen hos ett föremål som rör sig mot söder och avlänkas rakt till höger får snart en rörelse mot väster.

Fortsätter det att avlänkas blir rörelsen snart mot norr, sedan mot öster och efterhand återigen mot söder. Jordrotationen har alltså den oväntade egenskapen att söka driva in all rörelse på jordytan i cirklar, se figur 3.

Om golfbollen i figur 2 kunde rulla utan friktion, skulle den komma tillbaka till spelaren efter 14 timmar, sedan den fullbordat en jättelik cirkelrörelse med 16 km radie. Jordrotationens förmåga att söka återföra all rörelse till utgångspunkten, är av avgörande betydelse för atmosfärens vindar och oceanernas strömmar.